1. 구간 합(Prefix sum)이란?
수열에서 특정 구간의 합을 구할 때 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘이다. 코딩 테스트에서 유용하게 활용 가능하니 꼭 알고 넘어가야 하는 알고리즘 중 하나이다.
부분 합과 혼동할 수 있어 정리해보자면, 일차원 배열 A가 있다고 하자.
- 부분 합(Partial sum) : 처음부터 k번 인덱스까지의 합 ( = A[0] + A[1] + ... A[k] )
- 구간 합(Prefix sum) : i번부터 j번 인덱스까지의 합 ( = A[i] + A[i+1] ... + A[j-1] + A[j] )
반복문으로 i번부터 j번 인덱스까지 더한다면?
#include <iostream>
using namespace std;
int main() {
int i, j;
cin >> i >> j;
int arr[5] = { 1, 2, 3, 4, 5 };
int sum = 0;
for (int k = i; k <= j; k++) {
sum += arr[k];
}
cout << sum;
}
사실 이렇게 구하는 방법이 훨씬 간단한 코드로 구현할 수 있다.
하지만 더해야 하는 구간의 길이가 매우 커질 경우, 그만큼 수행해야 하는 연산도 늘어나기 때문에 정해진 시간 내에 해결할 수 없다. 위와 같이 반복문을 이용하여 arr[i] ~ arr[j] 까지 더하는 알고리즘의 시간 복잡도는 O(n)이다.
2. 구간 합 알고리즘 구현하기
① 합 배열 만들기
구간 합 알고리즘을 사용하기 위해서는 "합 배열"이라는 배열을 만들어야 한다.

합 배열 sum은 기존의 배열을 이용하여 만들면 된다. sum[i]는 기존 배열 arr의 0번 인덱스부터 i번 인덱스까지의 합이다.(누적 합과 같다) sum을 선언할 때 0으로 초기화하여 선언한 후, arr에 i번째 값이 들어올 때마다 sum[i]에 arr을 더해주면 된다.
sum[ i ] = sum[ i - 1 ] + arr[ i ];
추가로, arr은 굳이 배열로 선언하여 입력받을 필요 없이, 반복문 안에서 해당 횟수만큼 입력받은 후 sum에 더해주기만 하면 된다. 아래 코드를 참고하자.
#include <iostream>
using namespace std;
int main() {
int sum[7] = {}; //sum[5] 원소를 모두 0으로 초기화
cout << "arr : ";
for (int i = 1; i <= 6; i++) {
int arr;
cin >> arr;
sum[i] = sum[i - 1] + arr; //새 입력이 들어올 때마다 sum[i-1]에 더해서 sum[i]에 대입
}
cout << "\n" << "sum : ";
for (int i = 1; i <= 6; i++) {
cout << sum[i] << " ";
}
}
② 합 배열을 이용하여 구간 합 구하기
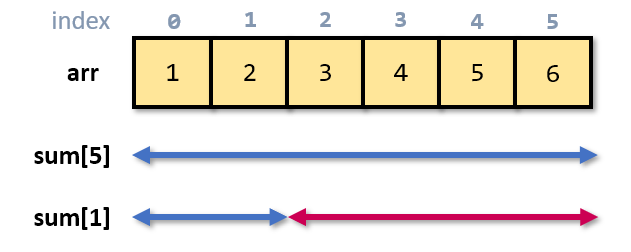
// i 에서 j 까지의 구간 합
sum[ j ] - sum[ i - 1 ];
합 배열 sum을 만들었으면, 이제 구간 합을 구하는건 쉽다. i번 인덱스부터 j번 인덱스까지의 구간 합은, sum[ j ] 에서 sum[ i - 1 ] 을 빼주면 된다. i번 인덱스 위치의 값도 포함해야 하므로 sum[ i ]가 아닌 sum[ i - 1 ]을 빼주어야 함에 주의하자.
cout << "1~3까지의 구간 합 : " << sum[3] - sum[0] << "\n";
cout << "2~5까지의 구간 합 : " << sum[5] - sum[1] << "\n";
cout << "4~6까지의 구간 합 : " << sum[6] - sum[3] << "\n";
따라서 합 배열만 구해놓으면 구간 합은 단순히 뺄셈 1회만 수행하면 된다. 즉 구간 합 알고리즘의 시간 복잡도는 O(1)로 매우 효율적인 알고리즘이라고 할 수 있다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] - 쉘 정렬 (Shell-sort) (0) | 2024.04.14 |
|---|---|
| [알고리즘] - 삽입 정렬 (Insertion-sort) (0) | 2024.04.09 |
| [알고리즘] - 선택 정렬 (Selection Sort) (0) | 2024.04.09 |
| [알고리즘] - 버블 정렬 (bubble sort) (1) | 2024.02.13 |
| [알고리즘] - 투 포인터 (Two-Pointers) (1) | 2024.01.19 |



